
日常生活中的加密,例如银行转账、身份识别、在线浏览,邮箱登录等,加密方式都采用的是RSA密钥。RSA密钥采用的是一种非对称加密算法。在公开密钥加密和电子商业中RSA被广泛使用。在这里我们不详细讨论RSA密钥的加密过程,只举一个例子加以说明。

假设存在爱丽丝和鲍伯两个人,鲍伯想给爱丽丝一条信息,但是又不想被第三方窃听。那么他们两人通过RSA密钥的加密解密过程大体上相当于以下的步骤:爱丽丝给鲍伯一个开着的保险箱,这个开着的保险箱相当于是RSA密钥中的公钥,保险箱的密码只有爱丽丝知道,这相当于是RSA密钥中的私钥。然后鲍伯把需要加密的信息放入这个保险箱,然后关上保险箱,这就相当于用公钥对信息进行了加密。然后鲍伯可以放心的把保险箱交给爱丽丝而不用担心信息泄露,因为除了爱丽丝之外,其他人不知道保险箱的密码。
就像没有绝对安全的保险箱一样,现有的RSA密钥也不是绝对安全的,它的安全性是由计算复杂度来保证的。例如,按照现在最快的电脑——神威·太湖之光超级计算机,破解一个1024比特的RSA密钥(目前比较常见的长度)也需要年,大概就是500万年的样子,因此一般认为RSA密钥是安全的。但是这只是对于经典计算机来说是正确的,对于量子计算机就不一定了。

传统的破解RSA密钥的方式是暴力破解,也就是通过计算机去逐个去穷尽所有的可能。这就需要去尝试所有可能的质数组合,因此需要很长的时间。
舒尔(Shor)算法的出现从根本上改变了这种情况。舒尔算法是一种量子算法,是1994年由美国数学家彼得.舒尔发明的。这种量子算法利用了量子比特的叠加性,可以在短时间内破译RSA密钥。例如,对于1024比特的RSA密钥,大概只需要1.4×107秒,大概就是160天左右。也就是说,大概只用半年左右的时间就能破译目前世界上最常用的密钥系统,这就是舒尔算法的强大之处。
舒尔算法的量子线路非常简单,如下图所示:
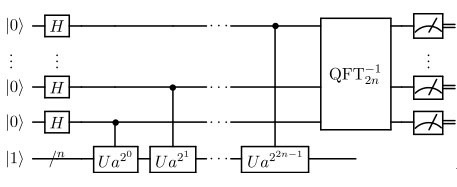
图中的U代表一些具体的量子门,QFT-1表示的是量子逆傅里叶变换。通过以上的量子线路使得输入的量子比特产生叠加和纠缠,然后利用量子比特的叠加性和纠缠性,舒尔算法可以在很短的时间破译RSA密钥。假定要分解的大数为N,舒尔算法的具体步骤如下:
(1)随机选取整数a(a
(2)若T为奇数,则返回1,重新选取a;若T为偶数,则取.
(3)求得y后,用欧几里德辗转相除法求得y-1,y+1与N的最大公约,则可以找到质因子p,q使得N=pq。
舒尔算法关键的地方就在于它能有效的计算的周期T,这就大大的缩短了求N的质因子所需的时间。
舒尔算法的出现使得人们意识到了量子计算机的强大性,也使得各国政府和学术界开始重视对量子信息,量子计算的研究。
不过,现在我们并不需要担心量子计算机和舒尔算法给传统RSA密钥带来的威胁,因为破译现有的RSA密钥需要量子计算机上有上千个量子比特同时运行才能实现,在现有的技术条件下,我们只能勉强实现对10个左右的量子比特的操作,更不用说上千个量子比特了。但是,这并不代表量子计算机距离我们很远,想想我们从第一台运算速度只有几千的电子计算机到现在运算速度达到亿亿次的超级计算机,只用了半个多世纪的时间,对于量子计算机,也许时间会更短。